Grundkonstruktionen Teil 2 (Geometrie)

An dieser Station erwartet Sie

Mathematik:

Eine "Winkelkonstruktion"

Bedienung:

Eine Strecke fester Länge zu konstruieren
Einen Winkel mit vorgegebener Größe zu konstruieren
Einen vorgegebenen Winkel zu übertragen

Das Dokument: Station_6_Grundkonstruktionen_Geometrie_2.tns

Das Dokument hat insgesamt 4 Seiten.

! Übertragen Sie das Dokument zuerst mit der PC-Software auf das Handheld in den Ordner "Eigene Dateien"(am besten in einen Unterordner "Lernstationen").

Aufgabe

Öffnen Sie die Datei "Station_6_Grundkonstruktionen_Geometrie_2.tns".
Bearbeiten Sie dann die Aufgabenstellungen, die auf den vier Registerblättern stehen.

Lösung der Aufgabe: Kurze Version

Sie möchten...	Applikation	Diese Schritte sollten Sie mit dem Rechner gehen...
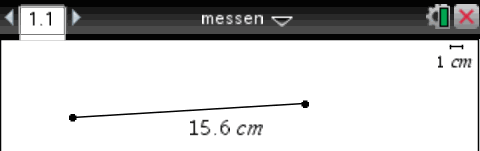
Eine Strecke mit fester Länge konstruieren	Geometry	Konstruieren einer Strecke. [, 4: Punkte & Geraden, 5: Strecke, ] Danach mit dem Touchpad den Mauszeiger auf die Strecke bringen und , 8: Messung, 1: Länge drücken. Auf den Text klicken, ein weiteres Mal klicken und den Text in z.B. 5 cm verändern.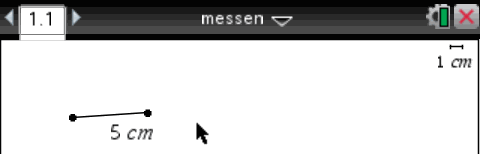
Einen Winkel mit vorgegebener Größe konstruieren	Geometry	Das geht nicht direkt! Bzw. es geht zwar auch direkt, nur ist dann die Konstruktion nicht mehr beliebig verschiebbar. Wenn das nicht stört, dann ist das die geeignete Konstruktion: Textfeld erstellen mit , 5: Text und den Wert eingeben, z.B. 40 für 40° Eine Strecke zeichnen , 8: Abbildung, 4: Drehung Auf die Strecke klicken auf den Punkt klicken, an dem der Winkel liegen soll auf den Text 40 klicken Will man die Winkelgröße ändern, kann der Text geändert werden. Sie können nun zwar die Ausgangsstrecke, nicht aber mehr den Punkt, an dem der Winkel liegt, verschieben. Übertragen Sie den Winkel, so ist bei dem übertragenen Objekt alles frei beweglich. Wollen Sie den Winkel fixieren, so müssen Sie den Text mit anklicken, 2: Attribute, auf das Schloss, Pfeiltaste nach rechts .
Einen vorgegeben Winkel an eine beliebige Gerade o.Ä. übertragen	Geometry	Gegeben sind s1 und s2 als Schenkel eines Winkels mit Scheitelpunkt S. Kreis k(S,r), r beliebig S1=s1∩k und S2=s2∩k Gerade g(A,B1) [Diesen zweiten Punkt, der die Gerade g festlegt, zeigt der Nspire nicht an, zur Konstruktion gehört er aber dazu!] Für die folgenden Kreise , 7: Konstruktion, 7: Zirkel verwenden: Kreis k1(A,r), [r ist die Länge der Strecke SS1; beim Zirkel zuerst S, dann S1 anklicken] B2=k1∩g Kreis k2(B2,Strecke S1S2) B3=k1∩k2 Gerade h(A,B3) Winkel zwischen g und h ist der vorgegebene Winkel.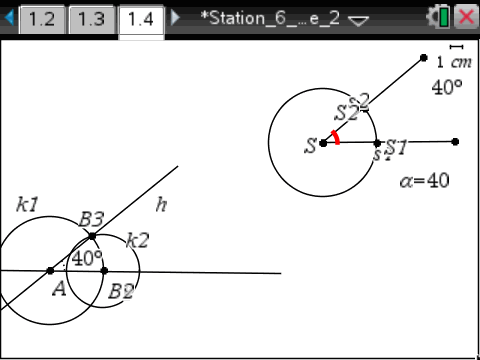