Dies ist das Onlinekompendium zum TI Nspire™ CX CAS des IMBF

Binomialverteilung (alle Werte bzw. einzelne Werte bestimmen) sowie kumulierte Binomialverteilung


Befehl: binompdf(n,p) / binompdf (n,p,k) bzw. binomcdf(n,p,untere Schranke,obere Schranke)Tastenkombination: 1, Menü, 5:Wahrscheinlichkeit, 5:Verteilungen, D:Binomial PDF bzw. E:Binomial CDF
Beispiel: binompdf(10,1/6) / binompdf (10,1/6,0) bzw. binomcdf(10,1/6,0,1)Veranstaltungen: Daten und Zufall

  • Binomialverteilung: binompdf(n,p)

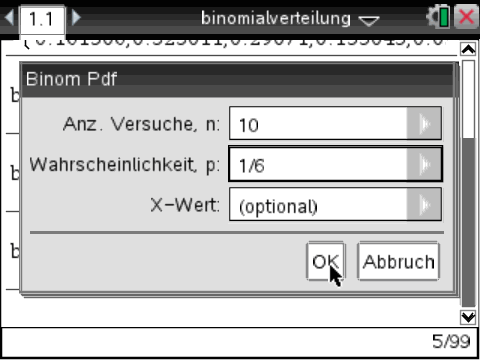
    • Um bei einer binomialverteilten Zufallsgröße die Wahrscheinlichkeitsverteilung bestimmen zu können, im Calculator auf Menü, 5: Wahrscheinlichkeit, 5: Verteilungen, E: Binom PDF gehen.

    Nun kann man in die Felder zuerst "n", die Anzahl der Versuche, und dann "p", die Wahrscheinlichkeit, mit der ein Ereignis eintritt, eingegeben werden. Die Eingaben mit Enter bestätigen.

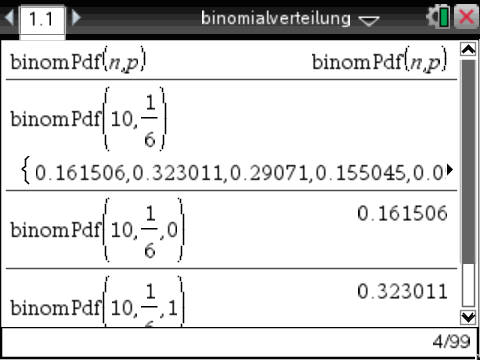
    In diesem Fall handelt es sich bespielsweise um die Zufallsgröße X: Anzahl der 4-er beim 10-fachen Wurf mit einem normalen Würfel. Die Wahrscheinlichkeit, eine 4 zu würfeln, liegt somit bei p = 1/6.

    Bestätigt man nun die Eingaben mit Enter, so erhält man die gesuchte Wahrscheinlichkeitsverteilung als Liste mit n+1 Werten. Der erste Wert der Liste entspricht der Wahrscheinlichkeit, dass bei 10 Würfen 0 4-er gewürfelt werden (der zweite Wert, dass eine 4 gewürfelt wird, etc.).

    Möchte man die Wahrscheinlichkeit dafür bestimmen, dass z.B. genau eine 4 gewürfelt wird, so kann man bei der Eingabe zusätzlich zu "n" und "p" auch noch einen ensprechenden X-Wert angeben. Die Wahrscheinlichkeit beträgt in diesem Fall P(X=1) = 0,323.



  • Kumulierte Binomialverteilung: binomcdf(n,p,untere Schranke,obere Schranke)

    • Um die kumulierte Wahrscheinlichkeit zu berechnen, im Calculator auf Menü, 5: Wahrscheinlichkeit, 5: Verteilungen, D: Binom CDF gehen.

    Neben den Parametern "n" und "p" nun auch die Schranken eingeben und mit Enter bestätigen.

    Gibt man als Schranken bespielsweise 0 und 1 an, so werden die Häufigkeiten von P(X=0) und P(X=1) aufsummiert. Es handelt sich also um die Wahrscheinlichkeit für P(X<=1). In diesem Beispiel läge die Wahrscheinlichkeit, dass bei 10 Würfen mit dem normalen Würfel maximal einmal die 4 fällt, bei P(X<=1) = 0,4845.