|
zum aktiven
Entdecken und selbststndigen Erarbeiten |
|
Erlebnis Algebra zum aktiven
Entdecken und selbststndigen
Erarbeiten |
|
||
|
In diesem
Buch lernen Sie dazu die Welt der natürlichen Zahlen und ihrer vielfältigen
Muster und Strukturen kennen. Und das auf eine Weise, wie Sie sich auch wünschen,
dass Ihre Schülerinnen und Schüler Mathematik betreiben. Sie lernen
keine trockenen Fakten, sondern werden eingeladen zu einer mathematischen
Entdeckungsreise. Durch viele interessante Probleme werden Sie angeregt,
Zahlen und ihre Strukturen selbstständig zu erforschen. In leicht zugänglichen
und unterhalt- samen Texten können Sie ihre Erfahrungen dann
reflektieren und zu einem fundierten und systematischen Wissen über die
Grundlagen der Arithmetik ausbauen. Nach der
Lektüre dieses Buches haben Sie nicht nur einen fundierten Überblick
über den Kosmos der natürlichen Zahlen bekommen, sondern auch
erfahren, was es bedeutet, eigenaktiv mathematische Entdeckungen zu machen.
Sie haben sich dabei Problemlösestrategien und Beweistechniken
angeeignet und auch gelernt, wann und wozu mathematische Formelsprache
hilfreich ist. Lsungen zu Kapitel 1-8 (ohne 6)
(40MB) Zu allen
Kapiteln werden Hinweise zu den Erkundungen und Lsungsmglichkeiten aller
bungen angeboten. (Hinweise auf Fehler oder Unklarheiten nehme ich gerne
entgegen). |
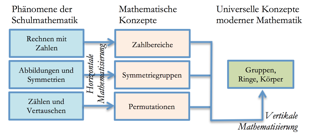
In diesem
Buch lernen Sie, wie die Ideen moderner Mathematik mit den mathematischen
Konzepten aus der Schule zusammenhngen. Sie erleben, wie durch mathematische
Abstraktion das Gemeinsame aus den Inhaltsbereichen der Schule, aus
Arithmetik, Kombinatorik, Geometrie und Gleichungsalgebra hervortritt. Dabei
begegnen Sie immer wieder denselben universellen Strukturen, die in der
Mathematik als "Gruppen", "Ringe" oder "Krper"
beschrieben werden. Sie lernen
keine trockenen Fakten, sondern verstehen Hintergrnde und bauen Brcken von
der Schulmathematik zur modernen Mathematik. Sie werden eingeladen zu einer mathematischen
Entdeckungsreise und zur selbststndigen Erforschung mathematischer
Strukturen. In leicht zugnglichen Texten knnen Sie Ihre Erfahrungen dann
reflektieren und zu einem fundierten und systematischen Wissen ber die
Kernideen der Algebra ausbauen.
|
||||
|
Diese
Materialien enthalten vor allem Bilder und Grafiken, die fr
Projektionsfolien oder bungszettel verwendet werden knnen. Interaktive Computerprogramme (Geogebra) |
Interaktive Computerprogramme (5MB) Zu den
Erkundungen (und auch zu anderen Abschnitten des Buches) gibt es Computerprogramme,
die das interaktive Explorieren untersttzen und die mathematischen Konzepte
anschaulich visualisieren. Alle Computerprogramme basieren auf der Software GeoGebra (Version 5) und Cinderella (Version 2). www.geogebra.de www.cinderella.de Hinweis fr CINDERELLA:Bitte
unbedingt die neuste Fasung unter http://beta.cinderella.de/public
herunterladen! |
||||
|
|
Kapitel 1
|
|
|||
|
|
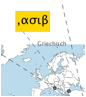
Zahlsysteme der Welt auf einer Interaktiven Karte. Zahlen werden automatisch bersetzt, der Aufbau der Zahlsysteme kann
erkundet werden. |
|
Erkundung der Wirkung von mehrfachem Spiegeln an zwei Spiegeln
|
||
|
|
|
Kapitel 2
|
|
||
|
|
Der Wurf einer Kugel am Galtonbrett wird simuliert. |
|
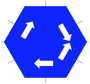
Erkundung der Symmetrien von geometrischen Figuren anhand von
Drehungen und Spiegelungen
|
||
|
|
Man kann eine Pyramide auf verschiedene Weise auseinandernehmen und
so unterschiedliche Summenformeln entdecken und erklren. |
|
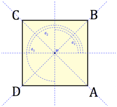
Erkundung der Verknpfung von Drehungen und Spiegelungen am Quadrat
|
||
|
|
Ein Spirograph wird simuliert. An ihm kann man untersuchen, wie sich
die Zahl der Zhne auf die entstehenden Muster auswirkt. |
|
Verkehrszeichen fr die Erkundung von Symmetriebrechung
|
||
|
|
|
Untersuchung der Symmetriegruppe
|
|||
|
|
Kapitel 3
|
|
|||
|
|
|
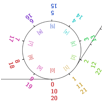
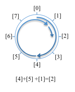
Erkundung von Mustern bei der Addition und Multiplikation mit Rest
|
|||
|
|
|
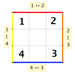
Visualisierung zum Rechnen mit Restklassen
|
|||
|
|
|
Visualisierung, wie Vielfache von Restklassen einfache Untergruppen
erzeugen. |
|||
|
|
|
Simulation von John Conways ãGame of LifeÒ mit verschiedenen Regeln
als Anwendung von Restklassenarithmetik
|
|||
|
|
|
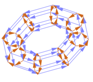
Visualisierung eines Produktes zweier zyklischer Gruppen als ein-
und aufklappbarer Torus
|
|||
|
|
|
Spiel ãMerlinÒ (oder ãLight-outÒ) – Welche Felder muss man
drcken, um alle grnen Lichter zu lschen? Anwendung von
Restklassenarithmetik. |
|||
|
|
Kapitel 4
|
|
|||
|
|
|
Erkundung der Verknpfung von Vertauschungen am Beispiel eines
zweidimensionalen ãZauberwrfelsÒ
|
|||
|
|
|
Erkundung der Drehungen, Spiegelungen und weiterer Symmetrien des
Tetraeders an einem 3D-Modell (auch mit 3D-Brille)
|
|||
|
|
|
Untersuchung der Schiebepuzzles (ã15-PuzzleÒ) auf Lsbarkeit und
Lsungswege – auch an einfacheren Beispielen
|
|||
|
|
Kapitel 5
|
|
|||
|
|
|
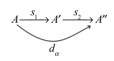
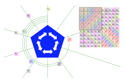
Erkundung von Gruppenstrukturen und Untergruppen mit Hilfe von Pfeildiagrammen
(Cayleydiagramme)
|
|||
|
|
|
Programm zur flexiblen Darstellung von Verknpfungstabellen von
endlichen Gruppen und deren Untergruppen und Nebenklassen |
|||
|
|
Kapitel 6
|
|
|||
|
|
|
Erkundung der Wirkungsweise verschiedener ebener Abbildungen und
ihrer Verknpfungen (Drehung, Spiegelung, Streckung, Scherung etc..) |
|||
|
|
|
Visualisierung einer Drehung in der Ebene mit Erklrung der Struktur
der Drehmatrix |
|||
|
|
|
Erkundung der Wirkungsweise der Matrix einer linearen Abbildung
(Drehung, Spiegelung, Streckung, Scherung etc..)
|
|||
|
|
|
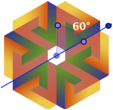
Erkundung der Symmetrien ebener Muster (Parkette, Kacheln, Tapeten)
|
|||
|
|
|
Visualisierung aller 15 Tapetengruppen, mit Kacheln und
Zufallsmustern |
|||
|
|
|
Erkundung der Erzeugung eines Kristalls aus elementaren
Verschiebungen und Drehungen. Finden einer Begrndung fr ãkristallographische
RestriktionÒ (nur 2,3,4,6-zhlige Symmetrie) |
|||
|
|
|
Erzeugung eines Parkettes im Stil von M.C. Escher durch Vernderung
einer Kachel |
|||
|
|
Kapitel 7
|
|
|||
|
|
|
Darstellung einer Kostruktion fr Strecken mit irrationaler Seitenlnge
mit Zirkel und Lineal. |
|||
|
|
|
Visualisierung einer Beziehung zur Herleitung der Caradnoschen
Formel (auch mit 3D-Brille)
|
|||
|
|
|
Erkundung von Operationen mit komplexen Zahlen (Additon, Multiplikation,
Wurzel, Potenz) ihrer geometrischen Interpretation (in der Gau§schen
Zahlenebene) |
|||
|
|
Kapitel 8
|
|
|||
|
|
|
Erkundung zu Teilern, Vielfachen und Primzalen unter den komplexen
ganzen Zahlen (Gau§sch Zahlen)
|
|||
|
|
|
Visualisierung eines Beweises fr den Fundamentalsatz der Algebra |
|||
|
|
Kapitel 9
|
|
|||
|
|
|
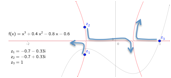
Erkundung der Anzahl und Lage der komplexen Nullstellen von
Polynomen
|
|||